Probleemide lahendamisel on oluline teada kuidas erinevad tegevused, nähtused on omavahel seotud. Mis juhtub, kui ma keeran selle kraani kinni? Mis juhtub, kui me protsessis ei kasuta survena 4 bari vaid 5 bari? Kui palju pikeneb protsessiaeg, kui ma kasutan 80 kraadise vee asemel 60 kraadist vett?
Aeg-ajalt tekib ajurünnaku käigus hüpoteese, kus väidetakse eksisteerivat mingi seos. See võib nii olla, võib ka mitte. Seost saab kontrollida hajuvusdiagrammiga, mis on üks seitsmest lihtsast kvaliteedijuhtimise tööriistast.
Seda saab kasutada, kui mõlema parameetri andmed on numbriliselt väljendatavad ning nad on pidevad. See tähendab nad ei ole loend, ei ole binaarsed a’la “Jah/ei” ning üks andmeridadest ei ole andmetesilt (operaator1, operaator2….). Sa ei saa seda kasutada näiteks selgitamaks, kas rohelistel toodetel on rohkem defekte kui punastel – selle jaoks on stratifitseerimine ja Pareto diagrammid.
Mõõtmine
Seose tugevuse mõõtmiseks peaksid sul olema kindlal ajahetkel fikseeritud 2 faktorit – mis iganes suurus x ja suurus y. Ma väga ei keskenduks siinkohal korrelatsioonifaktori käsitsi arvutamisele – mõistlikum on minna lihtsama vastupanu teed ja kasutada Exceli funktsioone.
Üldjuhul peaks valimi suurus olema vähemalt 25-50 andmepunkti ning teadupärast saab olla korrelatsioonikordaja vahemikus -1…0…1. Seose olemasolu võib aimata kui korrelatsiooni kordaja on vahemikkudes -1….-0,65 ja 0,65…1. Kui korrellatsioonikordaja jääb nende vahele, siis võiks öelda, et seost nagu ei ole. Päris tõsikindlalt seda siiski väita ei saa.
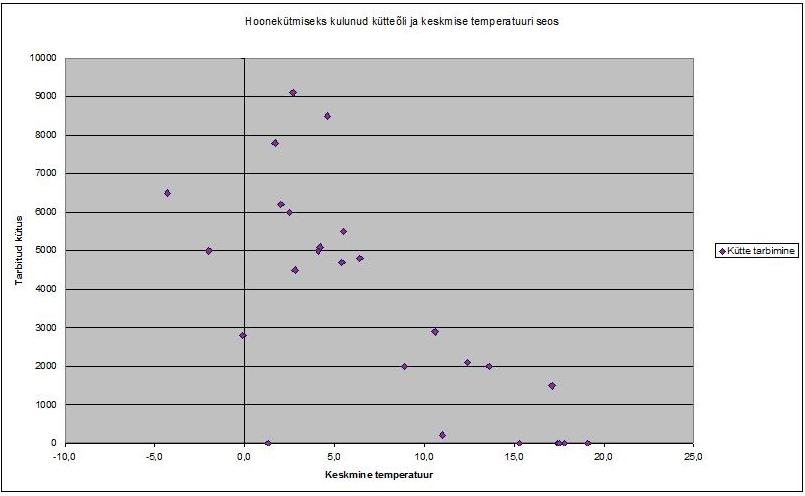
Vaatame ühte päriselulist näidet:
X-teljel on siis kuu keskmine temperatuur ning Y-teljel hoone kütmiseks ärakulutatud kütusekogus kuus. Korrelatsioonikordaja on -0,73, mis ütleb, et seos on olemas. Mis peamine – see on ka loogiline – temperatuuri langedes kasvavad küttekulud.
Vahemärkusena – selliseid ilusaid õpikunäiteid, kus punktiparv on ilusasti 45-kraadise nurga all üht või teistpidi püsti, pole mina veel suutnud päris elus näha. Märksa tõenäolisem on ülaltoodud pilt.
Küsimused, mida pead endalt küsima hajuvusdiagrammi tõlgendamisel:
- Kuidas ja mis hetkel sa oma andmed saad? Kuigi ülaltoodud näites on korrelatsioon küllaltki tugev, siis kütusekulu on võetud mahutisse valamise hetkest, mitte reaalselt põletamise hetkest. Kuivõrd mahuti oli aga 3000 liitrit, siis see solgib andmeid päris kõvasti, sest ei peegelda väga täpselt reaalselt selles kuus katlamajas põletatud kütuse hulka.
- Mida andmed sisaldavad? Tegelikult põletati kütust ka olmevee soojendamiseks. Kui suur selle osa on? Stratifitseerimine on oluline tööriist ka hajuvusdiagrammi koostamisel.
- Kui stabiilne on süsteem olnud? Antud näite puhul oli kõik väga stabiilne. Kogu perioodi vältel juhtis maja kütmist automaatika, mille töörežiimi ei muudetud. Mingeid eritöid soojustuse parendamiseks ei tehtud. Reaalses elus ajalooliste andmete töötlemisel on sul siiski väga harva selline stabiilsus olemas. Pigem on tõenäoline, et vähemalt korra aastas on toimunud mingi šokk, mingi suurem muudatus. Eriti tõenäoline on see siis, kui protsess on oluline ning omab suurt mõju ettevõtte kasumlikkusele.
- Kas tulemus on loogiline? Mõnikord käib tulemus risti-vastu sellele, mis on loogiline. Vahest see ongi niimoodi aga võimalik on, et seose puudumist seletavad eelnevad kolm küsimust.
- Mis tegelikult põhjustab mida? TTÜ väidab, et nende ülikoolist tulevad tipud. TTÜ uhke vilistlasena oletame, et see väide on tõene. Mis aga seda põhjustab? On see turundus, mis meelitab endale Vabariigi parimad abituriendid? On see vastuvõtmise protseduur, mis jätab nõrgemad ukse taha? Või on see erakordselt kõrge õpetamise ja teaduse tegemise tase? Korrelatsioonianalüüs ei vasta küsimusele “miks?”, selle pead sa ise välja mõtlema.
- Millal miski midagi põhjustab? Lähme näitega korraks kvaliteedijuhtimisest kaugemale. Kui su müügimeeskond teeb keskmiselt ühes kuus igapäevaselt 50 esmakohtumist päevas ning see number suureneb või väheneb, siis millal see hakkab mõjutama müügikäivet? Millal see hakkab mõjutama kulusid iga tehtud lepingu kohta? On ilmselge, et selle müügikäive muutub viiteajaga. Mul on olnud situatsioone, kus ühe andmerea kahenädalase nihutamisega kasvas korrelatsioonikordaja 0,45 -> 0,68. Ehk siis seose puudumiselt, mingi seose olemasoluni.
Kokkuvõtteks
Hajuvusdiagramm võib olla väga võimas tööriist mõistmaks, mis sul üldse ettevõttes toimub. See ei ole siiski päris ohutu – sa pead siiski arvestama kõikvõimalike eksimustega. Korrelatsiooni olemasolu võib tähendada seose olemasolu, võib ka mitte. Veidral kombel ei tähenda ka korrelatsiooni puudumine seose puudumist. Võib-olla sa pole lihtsalt õigeid andmeid õigesti kasutanud. Mis iganes. Kasuta igatahes aga ole ettevaatlik, et jalga ei tulistaks.